PEMODELAN FARMAKOKINETIK DASAR (part 2)

Oke guys, sekarang mau lanjut postingan part 2 (yang belum lihat part 1, biar nyambung bisa dicek di link ini) dari pemodelan farmakokinetik. Ini sih main pointnya, so lets get start it

Oke, sebelumnya aku mau kasi tips, dari hasil surve untuk beberapa orang, mereka lebih suka pakai persamaan ln, bedanya hanya pencarian nilai k, yang mana k dengan persamaan log perlu dikali 2,3 sedangkan ln tidak, pada pembahasan ini akan menggunakan persamaan ln ya

Untuk pembahasan kompartemen 1 dan 2 akan lebih digunakan orde 1, karena umumnya orde inilah yang digunakan

2. Kompartemen I Intravena

Intravena ciri khasnya adalah jumlah obat awal merupakan kadar obat yang tertinggi dalam plasma. Kenapa bisa begitu, ya karena obatnya memang langsung disuntikkan ke aliran darah jadi tidak mengalami proses absorpsi terlebih dahulu. Pengerjaan kompartemen I ini mudah lho apabila dipahami baik-baik langkah demi langkah, jadi kita bahas dengan soal saja ya, soal ini diperoleh dari link ini

Langkah 1:

BB pasien = 50 kg; dosis obat = 200 mg/kg, apabila ada soal dengan dosis seperti ini jangan lupa dikali terlebih dahulu ya untuk memperoleh dosis pemberiannya, bisa dilihat dari satuannya, yang mana untuk menapatkan satuan mg kita harus mengalikan BB pasien dengan dosis obat, sehingga dosis pemeriannya adalah 1000 mg

Langkah 2:

Untuk memastikan orde yang digunakan dalam soal, maka dapat diawali dengan menghitung nilai r dari hubungan t dengan Cp, yang mana dari soal ini diperoleh hasil, r^2 = 0,832 yang menunjukkan bahwa hubungan ini tidak linier (orde 1), cara menghitungnya gunakan kalkulator ilmiah ya

Langkah 3:

Buatlah nilai ln dari data Cp pada soal, sehingga diperoleh nilai sebagai berikut:

Untuk menyederhanakan hitungan, nilai dibelakang koma bisa disederhanakan menjadi 2-3 angka dibelakang koma

Langkah 4:

Buatlah grafik untuk menentukan kompartemennya, ini penting dilakukan, karena tanpa dibuat grafik kalian tidak bisa menentukan ini kompartemen berapa, grafik secara manual bisa dibuat dengan milimeter blok, atau dengan semilog (pada penggunaan semi log langsung dimasukkan nilai t dan Cp, akan langsung diekstrapolasikan sendiri oleh grafiknya), file semilog bisa kalian download di link ini ya

Grafik yang diperoleh adalah sebagai berikut:

Dari nilai r sudah bisa dibedakan, hasil ekstrapolasi menunjukkan nilai r^2 = 1. Kompartemen ini dikatakan merupakan kompartemen 1 karena terdiri dari 1 fase saja, yaitu eliminasi yang ditunjukkan dengan liniernya kurva yang diperoleh, jadi dari sini cukup hanya dilakukan perhitungan untuk fase eliminasi saja

Langkah 5:

Tentukan persamaan farmakokinetiknya. Persamaan farmakokinetik diperoleh dari persamaan regresi dari hubungan t dengan lnCp, yaitu: y = -0,689x + 1,601, maka persamaan farmakokinetiknya adalah lnCp = -0,698t + 1,601

Langkah 6:

Menghitung parameter farmakokinetik, yay, ini adalah langkah terakhir. Parameter farmakokinetik yang dihitung pada kompartemen I IV adalah:

a. ke (konstanta eliminasi)

ke pada persamaan ln adalah: -ke = b

-ke = b

-ke = -0,689 (karena nilai b negatif)

ke = 0,689 /jam

b. Cp0 (konsentrasi plasma pada waktu 0)

Cp0 = e^a (anti ln a), maka

Cp0 = e^1,601

Cp0 = 4,958 mg/L

c. t 1/2 (waktu paruh)

t 1/2 = 0,693/ke

t 1/2 = 0,693/0,689

t 1/2 = 1,006 jam

d. Vd (Volume Distribusi)

Vd = D0/Cp0

Vd = 1000 mg/4,958 mg/L

Vd = 201,694 L

Vd juga bisa dihitung dengan, Vd = D0/(k.AUC)

e. AUC (area under curve)

AUC = Cp0/ke

AUC = 4,958 mg/L / 0,689/jam

AUC = 7,196 mg.jam/L

f. Cl (clearance)

Cl = ke. Vd

Cl = 0,689/jam . 201,694 L

Cl = 140,782 L/jam

Cl juga bisa dihitung dengan, Cl = D0/AUC

2. Kompartemen 2 Intravena

Kompartemen 2 ini mulai agak ribet, kenapa, karena harus pakai metode residual karena disini ada 2 fase, untuk lebih jelasnya bisa disimak dari soal berikut, soal ini diperoleh dari link ini ya

Langkah 1:

Pada soal ini dosis sudah diketahui 100 mg, jadi tidak perlu dilakukan perhitungan dosis lagi

Langkah 2:

Pastikan data bukan merupakan orde 0, dengan cara melihat hubungan antara t dengan Cp, yang mana nilai r^2 yang diperoleh adalah: 0,549, jadi dapat dipastikan bahwa ini merupaka orde 1

Langkah 3:

Tentukanlah nilai ln dari semua data pada grafik, sehingga diperoleh:

Langkah 4:

Buatlah grafik hubungan t dengan ln Cp sebagai berikut:

Dari grafik ini belum juga diperoleh regresi yang linier. Pada data ke 4 (t=1,4) mulai terjadi penurunan yang lebih landai, hal ini menunjukkan adanya 2 fase pada data ini (kompartemen 2) yang mana fase pertama merupakan fase distribusi (bagian atas), sedangkan bagian bawah merupakan fase eliminasi.

Langkah ke 5:
Disini kita mulai masuk kebagian residual, langkah awal kita harus menentukan persamaan regresi eliminasi yang linier, data yang linier dapat kita tentukan dengan melihat grafik. Pada grafik diatas kita dapat melihat bahwa data t4 - t16 menunjukkan hubungan yang linier.

Persamaan yang diperoleh dari data t4 - t16 adalah:

Just information, umumnya yang digunakan untuk memperoleh regresi linier adalah 3 data (untuk eliminasi dari bawah dan untuk distribusi atau absorpsi dari atas) namun, untuk beberapa khasus, seperti data ini, 4 data memberikan hasil yang linier, jadi tipsnya, coba gunakan 4 data terlebih dahulu dan bandingkan nilai r^2nya dengan 3 data, gunakan data yang memberikan nilai r^2 lebih medekati 1.

Langkah 6:

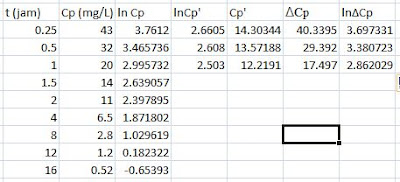
Menentukan persamaan regresi linier dari absorpsi. Caranya adalah dengan mencari nilai Cp' terlebih dahulu. Nilai Cp' diperoleh dari memasukkan nilai t absorpsi pada persamaan regresi eliminasi. Pada data ini digunakan 3 data teratas, yaitu t0,25 - t1. Ingat yang dicari adalah nilai Cp', sehingga nilai yang diperoleh dari perhitungan harus di anti lnkan. Langkah selanjutnya adalah menentukan ΔCp dengan cara mengurangi nilai Cp dengan Cp' (nilai ΔCp adalah mutlak). Setelah diperoleh ΔCp maka nilainya diubah kedalam bentuk ln, hingga diperoleh nilai lnΔCp. Nilai lnΔCp inilah yang kemudian dihubungakan dengan t untuk memperoleh persamaan regresi distribusi. Ringkasnya dapat dilihat dari tabel berikut:

Untuk memperjelas hasil yang diperoleh, juga dapat dilakukan penggambaran grafik dari data distribusi (hubungan t dan lnΔCp):

Persamaan regresi yang diperoleh akan digunakan untuk menentukan persamaan dan parameter dari farmakokinetik.

Langkah 7:

Persamaan farmakokinetik untuk kompartemen 2 IV merupakan penjumlahan dari fase distribusi dan eliminasi (cara mudah mengingatnya adalah kedua fase ini segaris yaitu menurun), sehingga persamaan farmakokinetiknya menjadi:

lnCp = (-kdt + lnCp0d) + (-ket + lnCp0e)

dengan persamaan distribusi : y = -1,102x + 3,956

dan persamaan eliminasi : y = -0,21x + 2,713

Dalam kompartemen 2 IV, kd disebut a, Cp0d sisebut A, ke disebut b, dan Cp0 e disebut B, maka persamaan farmakokinetik menjadi:

lnCp = (-at + lnA) + (-bt + lnB)

lnCp = (-1,102t + 3,956) + (-0,21t + 2,713)

Langkah 8:

Parameter farmakokinetik 

a. ke (konstanta eliminasi)
Nilai konstanta eliminasi dalam kompartemen 2 IV biasanya diistilahkan dengan b, sehingga:
b = -b (slope pada persamaan eliminasi)
b = - (-0,21)
b = 0,21/jam

b. Cp0 eliminasi = B
lnB (intersep pada persamaan eliminasi) = 2,713
B = 15,07 mg/L

c. te 1/2 (waktu paruh eliminasi)
te 1/2 = 0,693/ke
te 1/2 = 3,3 jam

d. kd (konstanta distribusi) = a
a = -b (slope pada persamaan distribusi)
a = -(-1,102)
a = 1,102 /jam

e. Cp0 distribusi = A
lnA (intersep pada persamaan distribusi) = 3,956
A = 19,22 mg/L

f. td 1/2 (waktu paruh distribusi)
td 1/2 = 0,693/kd
td 1/2 = 0,693/1,102
td 1/2 = 0,63 jam

g. Cp0 (konsentrasi pada waktu 0)
Cp0 = A + B (hubungan ini mengikuti persamaan dari kompartemen 2 IV)
Cp0 = 19,22 mg/L + 15,07 mg/L
Cp0 = 34,29 mg/L

h. AUC (area under curve)
AUC = A/a + B/b (hubungan yang digunakan juga mengikuti persamaan dari kompartemen 2 IV)
AUC = 19,22/1,102 + 15,07/0,21
AUC = 89,202 mg.jam/L

i. k (konstanta laju sentral)
k = ab(A + B)/Ab + Ba)
k = 0,21/jam x 1,102/jam (19,22 mg/L + 15,07 mg/L)/(19,22 mg/L x 0,21/jam) + (15,07 mg/L x 1,102/jam)
k = 0.23 (34.29)/4,04 + 16,61
k = 11,71/20,64
k =  0,57 /jam

j. k12 (konstanta laju sentral - perifer)
k12 = AB(b-a)^2/(A+B)(Ab + Ba)
k12 = 19,22  x 15,07 (1,102 - 0,31)/(34,29)(20,64)
k12 = 289,64 (0,792)/707,74
k12 = 0,32/jam

k. k21 (konstanta laju perifer - sentral)
k21 = Ab + Ba/A + B
k21 = 20,64/34,29
k21 = 0,602/jam

l. Vp (volume sentral)
Volume sentral ini memiliki rumus yang sama dengan volume distribusi pada IV kompartemen I
Vp = D0/Cp0
Vp = 100 mg/34,29 mg/L
Vp = 2,91 L

m. (Vd)ss (volume distribusi saat steady state)
(Vd)ss = Vp + (k12/k21)Vp
(Vd)ss = 2,91 + (0,32/0,602)2,91
(Vd)ss = 4,45 L

n. (Vd)eks (volume distribusi saat ekstrapolasi)
(Vd)eks = D0/B
(Vd)eks = 100/15,07
(Vd)eks = 6,63 L

o. (Vd)area (volume distribusi area)
(Vd)area = D0/b(AUC)
(Vd)area = 100/0,21(89,202)
(Vd)area = 5,34 L

Mengingat komparten 1 dan 2 untuk jalur IV saja sudah sangat panjang, jadi untuk kompartemen oralnya akan dilanjutkan minggu depan. So stay tune ^^. Happy sharing.
Kompartemen 2 oral dapat diakses di link berikut.